Electron properties
With the development of quantum mechanics and experimental findings (such as the two slit diffraction of electrons), it was found that the electrons orbiting a nucleus could not be fully described as particles, but needed to be explained by wave–particle duality. In this sense, electrons have the following properties:
Wave-like properties:
- Electrons do not orbit a nucleus in the manner of a planet orbiting a star, but instead exist as standing waves. Thus the lowest possible energy an electron can take is similar to the fundamental frequency of a wave on a string. Higher energy states are similar to harmonics of that fundamental frequency.
- The electrons are never in a single point location, though the probability of interacting with the electron at a single point can be found from the electron’s wave function. The electron’s charge acts like it is smeared out in space in a continuous distribution, proportional at any point to the squared magnitude of the electron’s wave function.
Particle-like properties:
Electrons retain particle-like properties such as: each wave state has the same electric charge as its electron particle. Each wave state has a single discrete spin (spin up or spin down) depending on its superposition.
The number of electrons orbiting a nucleus can be only an integer.
Electrons jump between orbitals like particles. For example, if one photon strikes the electrons, only one electron changes state as a result.
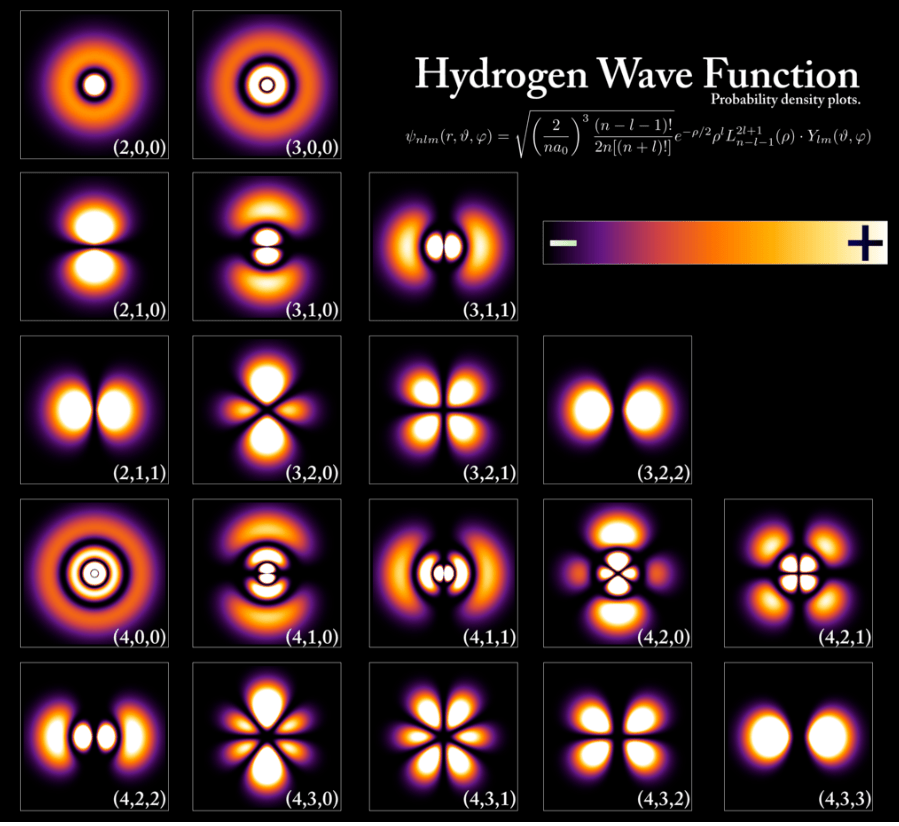
Hydrogen Wave Functions – Spherical
Schrodinger Equation – Time dependent

Schrodinger Equation – Time independent

Harmonic Oscillator for Schrodinger
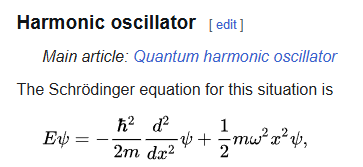
Spherical Polar Coordinates for Schrodinger

